TL;DR: You probably don't need DNNs, but you ABSOLUTELY SHOULD know and practice data analysis!
- Curse of dimensionality
Classical machine learning works on datasets of small or moderate number of dimensions. If you ever tried to do any function approximation or to work with optimization in general, you should have noticed that all these problems suffer from the "curse of dimensionality".
Say for example that we have a set of outdoor images of a fixed size: 256x128. And let's say that this set is labeled with a value that tells at what time of the day the image was taken. We can see this dataset as samples of an underlying function that takes as input 98304 (WxHxRGB) values and outputs one.
In theory, we could use standard function fitting to find an expression that in general can tell from any image the time it was taken, but in practice, this approach goes nowhere: it's very hard to find functional expressions in so many dimensions!
The classic machine learning approach to these problems is to do some manual feature selection. We can observe our data set and come up with some statistics that describe our images compactly, and that we know are useful for the problem at hand.
 |
| More dimensions, more directions, more saddles! |
We could, for example, compute the average color, thinking that different time of day does strongly change the overall tinting of the photos, or we could compute how much contrast we have, how many isolated bright pixels, all sorts of measures, then use or machine learning models on these.
The idea here is that there is a feedback loop between the data, the practitioner, and the algorithms. We look at the data set, make hypotheses on what could help reduce dimensionality, project, learn; if it didn't work well we rinse and repeat.
 |
| A scatterplot matrix can show which dimensions of a dataset have interesting correlations. |
This process is extremely useful, and it can help us understand the data better, discover relationships, invariants.
 |
| Multidimensional scaling, reducing a 3d data set to 1D |
The learning process can sometimes instruct the exploration as well: we can train on a given set of features we picked, then notice that the training didn't really use much some of them (e.g. they have very small weights in our functional expression), and in that case we know these features are not very useful for the task at hand.
Or we could use a variety of automated dimensionality reduction algorithms to create the features we want. Or we could use interactive data visualization to try to understand which "axes" have more interesting information...
- Deep learning
Deep learning goes a step forwards and tries to eliminate the manual feature engineering part of machine learning. In general, it refers to any machine learning technique that learns hierarchical features.
In the previous example we said it's very hard to learn directly from image pixels a given high-level feature, we have to engineer features first, do dimensionality reduction.
Deep learning comes and says, ok, we can't easily go from 98304 dimensions to time-of-day, but could we automatically go from 98304 dimensions to maybe 10000, which represent the data set well? It's a form of compression, can we do a bit of dimensionality reduction, so that the reduced data still retains most of the information of the original?
Well, of course, sure we can! Indeed we know how to do compression, we know how to do some dimensionality reduction automatically, no problem. But if we can do a bit of that, can we then keep going? Go from 10000 to 1000, from 1000 to 100, and from 100 to 10? Always nudging each layer so it keeps in mind that we want features that are good for a specific final objective? In other words, can we learn good features, recursively, thus eliminating the laborious process of data exploration and manual projection?
Turns out that with some trickery, we can.
 |
| DNN for face recognition, each layer learns higher-order features |
- Deep learning is hard
Why learning huge models fails? Try to picture the process: you have a very large vector of parameters to optimize, a point in a space of thousands, tens of thousands of dimensions. Each optimization step you want to choose a direction in which to move, you want to explore this space towards a minimum of the error function.
There are just so many possible choices, if you were to explore randomly, just try different directions, it would take forever. If before doing a step we were to try any possible direction, we would need to evaluate the error function at least once per dimension, thousands of times.
Your most reliable guide through these choices is the gradient of the error function, a big arrow telling in which direction the error is going to be smaller if a small step is taken. But computing the gradient of a big model itself is really hard, numerical errors can lead to the so-called gradient diffusion.
Think of a neural network with many, many layers. A choice (change, gradient) of a weight in the first layer will change the output in a very indirect way, it will alter a bit the output of the layer but that output will be fed into many others before reaching the destination, the final value of the neural network.
Think of a neural network with many, many layers. A choice (change, gradient) of a weight in the first layer will change the output in a very indirect way, it will alter a bit the output of the layer but that output will be fed into many others before reaching the destination, the final value of the neural network.
The relationship between the layers near the output and the output itself is more clear, we can observe the layer inputs and we know what the weights will do, but layers very far from the output contribute in such an indirect way!
Another problem is that the more complex the model is, the more data we need to train it. If we have a model with tens of thousands of parameters, but we have only a few data point, we can easily "overfit": learn an expression that perfectly approximates the data points we have, but that is not related to the underlying process that generated these data points, the function that we really wanted to learn and that we know only by examples!
In general, the more powerful we want our model to be, the more data we need to have. But obtaining the data, especially if we need labeled data, is often non-trivial!
Another problem is that the more complex the model is, the more data we need to train it. If we have a model with tens of thousands of parameters, but we have only a few data point, we can easily "overfit": learn an expression that perfectly approximates the data points we have, but that is not related to the underlying process that generated these data points, the function that we really wanted to learn and that we know only by examples!
 |
| Overfitting example. |
- The deep autoencoder
One idea that worked in the context of neural networks is to try to learn stuff layer-by-layer, instead of trying to train the whole network at once: enter the autoencoder.
An autoencoder is a neural network that instead of approximating a function that connects given inputs to some outputs, it connects inputs to themselves. In other words, the output of the neural network has to be the same as the inputs (or alternatively we can use a sparsity constraint on the weights). We can't just use an identity neural network though, the kink in this is that the autoencoder has to have a hidden layer with fewer neurons than the number of inputs!
 |
| Stacked autoencoder. |
This is perhaps surprisingly not hard, if the hidden layer bottleneck is not too small, we can just use backpropagation, follow the gradient, find all the weights we need.
The idea of the stacked autoencoder is to not stop at just one layer: once we train a first dimensionality-reduction NN we keep going by stripping the decoding layer (output) and connecting a second autoencoder to the hidden layer of the first one. And we can keep going from there, by the end, we'll have a deep network with many layers, each smaller than the preceding, each that has learned a bit of compression. Features!
The stacked autoencoder is unsupervised learning, we trained it without ever looking at our labels, but once trained nothing prevents us to do a final training pass in a supervised way. We might have gone from our thousands of dimensions to just a few, and there at the end, we can attach a regular neural network and train all the entire thing in a supervised way.
As the "difficult" layers, the ones very far from the outputs, have already learned some good features, the training will be much easier: the weights of these layers can still be affected by the optimization process, specializing to the dataset we have, but we know they already start in a good position, they have learned already features that in general are very expressive.
- Contemporary deep learning
More commonly today deep learning is not done via an unsupervised pre-training of the network, instead, we often are able to directly optimize bigger models. This has been possible via a better understanding of several components:
- The role of initialization: how to set the initial, randomized, set of weights.
- The role of the activation function shapes.
- Learning algorithms.
- Regularization.
We still use gradient descent type of algorithms, first-order local optimizers that use derivatives, but typically the optimizer uses approximate derivatives (stochastic gradient descent: the error is computed only with random subsets of the data) and tries to be smart (adagrad, adam, adadelta, rmsprop...) about how fast it should descend (the step size, also called learning rate).
In DNNs we don't really care about reaching a global optimum, it's expected for the model to have myriads of local minima (because of symmetries, of how weights can be permuted in ways that yield the same final solution), but reaching any of them can be hard. Saddle points are more common than local minima, and ill conditioning can make gradient descent not converge.
Regularization: how to reduce the generalization error.
Regularization: how to reduce the generalization error.
By far the most important principle though is regularization. The idea is to try to learn general models, that do not just perform well on the data we have, but that truly embody the underlying hidden function that generated it.
A basic regularization method that is almost always used with NNs is early stopping. By splitting the data in a training set (used to compute the error and the gradients) and a validation set (used to check that the solution is able to generalize): after some training iterations we might notice that the error on the training set keeps going down, but the one on the validation set starts rising, that's when overfitting is beginning to take place (and we should stop the training "early").
In general regularization it can be done by imposing constraints (often can be added to the error function as extra penalties) and biasing towards simpler models (think Occam's razor) that explain the data; we accept to perform a bit worse in terms of error on the training data set if in change we get a simpler, more general solution.
This is really the key to deep neural networks: we don't use small networks, we construct huge ones with a large number of parameters because we know that the underlying problem is complex, it's probably exceeding what a computer can solve exactly.
But at the same time, we steer our training so that our parameters try to be as sparse as possible; it has to have a cost to use a weight, to activate a circuit, this, in turn, ensures that when the network learns something, it's something important.
We know that we don't have lots of data compared to how big the problem is, we have only a few examples of a very general domain.
We know that we don't have lots of data compared to how big the problem is, we have only a few examples of a very general domain.
Other ways to make sure that the weights are "robust" is to inject noise, or to not always train with all of them but try cutting different parts of the network out as we train (dropout).
Think for example a deep neural network that has to learn how to recognize cats. We might have thousand of photos of cats, but still, there is really an infinite variety, we can't even enumerate all the possible cats in all possible poses, environments and so on, these are all infinite. And we know that in general we need a large model to learn about cats, recognizing complex shapes is something that requires quite some brain-power.
 |
| Google's famous "cat" DNN |
What we want though is to avoid that our model just learns to recognize exactly the handful of cats we showed it, we want it to extract some higher-level knowledge of what cats looks like.
Lastly, data augmentation can be used as well: we can always try to generate more data from a smaller set of examples. We can add noise and other "distractions" to make sure that we're not learning too much the specific examples provided.
Maybe we know that certain transforms are still valid examples of the same data, for example, a rotated cat is still a cat. A cat behind a pillar is still a cat or on different backgrounds. Or maybe we can't generate more data of a given kind, but we can generate "adversarial" data: examples of things that are not what we are seeking for.
Maybe we know that certain transforms are still valid examples of the same data, for example, a rotated cat is still a cat. A cat behind a pillar is still a cat or on different backgrounds. Or maybe we can't generate more data of a given kind, but we can generate "adversarial" data: examples of things that are not what we are seeking for.
- Do you need all this, in your daily job?
Today there is a ton of hype around deep learning and deep neural networks, with huge investments on all fronts. DNNs are groundbreaking in terms of their representation power and deep learning is even guiding the design of new GPUs and ad-hoc hardware! But, for all the fantastic accomplishments and great results we see, I'd say that most of the times we don't need it...
One key compromise we have with deep learning is that it replaces feature engineering with architecture engineering. True, we don't need to hand-craft features anymore, but this doesn't mean that things just work!
Finding the right architecture for a deep learning problem is hard, and it's still mostly and art done with experience and trials and errors.
Finding the right architecture for a deep learning problem is hard, and it's still mostly and art done with experience and trials and errors.
This might very well be a bad tradeoff. When we explore data and try to find good features we effectively learn (ourselves) some properties of the data. We make hypotheses about what might be significant and test them.
In contrast, deep neural networks are much more opaque and impenetrable (even if some progress has been made). And this is important, because it turns out that DNN can be easily fooled (even if this is being "solved" via adversarial learning).
In contrast, deep neural networks are much more opaque and impenetrable (even if some progress has been made). And this is important, because it turns out that DNN can be easily fooled (even if this is being "solved" via adversarial learning).
Architecture engineering also has slower iteration times, we have each time to train our architecture to see how it works, we need to tune the training algorithms themselves... In general building deep models is expensive, both in terms of human and machine time.
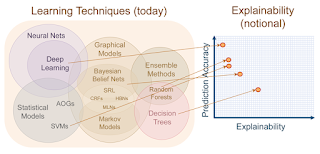 |
| Decision trees, forests, gradient boosting are much more explainable classifiers than DNNs |
And lastly, deep models will always require more data to train. The reason is simple: when we create statistical features ourselves, we're effectively giving the machine learning process some a-priori model. We know that some things make sense, correlate with our problem and that some others do not.
This a-priori information acts like a constraint: we restrict what we are looking for, but in exchange, we get fewer degrees of freedom and thus fewer data points can be used to fit our model.
This a-priori information acts like a constraint: we restrict what we are looking for, but in exchange, we get fewer degrees of freedom and thus fewer data points can be used to fit our model.
In deep learning, we want to discover features by using very powerful models. We want to extract very general knowledge from the data, and in order to do so, we need to show the machine learning algorithm lots of examples...
In the end, the real crux of the issue is that most likely, especially if you're not already working with data and machine learning on a problem, you don't need to use the most complex, state of the art weapon in the machine learning arsenal in order to have great results!
- Conclusions
The way I see all this is that we have a continuum of choices. On one end we have expert-driven solutions: we have a problem, we apply our intellect and we come with a formula or an algorithm that solves it. This is the conventional approach to (computer) science and when it works, it works great.
Sometimes the problems we need to solve are intractable: we might not have enough information, we might not have an underlying theoretical framework to work with, or we might simply not have in practice enough computational resources.
In these cases, we can find approximations: we make assumptions, effectively chipping away at the problem, constraining it into a simpler one that we know how to solve directly. Often it's easy to make somewhat reasonable assumption leading to good solutions. It's very hard though to know that the assumptions we made are the best possible.
On the other end, we have "ignorant", black-box solutions: we use computers to automatically discover, learn, how to deal with a problem, and our intelligence is applied catering to the learning process, not the underlying problem we're trying to solve.
If there are assumptions to be made, we hope that the black-box learning process will discover them automatically from the data, we don't provide any of our own reasoning.
This methodology can be very powerful and yield interesting results, as we didn't pose any limits, it might discover solutions we could have never imagined. On the other hand, it's also a huge waste: we are smart! Using our brain to chip away at a problem can definitely be better than hoping that an algorithm somehow will do something reasonable!
In between, we have an ocean of shades of data-driven solutions... It's like the old adage that one should not try to optimize a program without profiling, in general, we should say that we should not try to solve a problem without having observed it a lot, without having generated data and explored the data.
We can avoid making early assumptions: we just observe the data and try to generate as much data as possible, capturing everything we can. Then, from the data, we can find solutions. Maybe sometimes it will be obvious that a given conventional algorithm will work, we can discover through the data new facts about our problem, build a theoretical framework. Or maybe, other times, we will just be able to observe that for no clear reason our data has a given shape, and we can just approximate that and get a solution, even if we don't know exactly why...
Deep learning is truly great, but I think an even bigger benefit of the current DNN "hype", other than the novel solutions it's bringing, is that more generalist programmers are exposed to the idea of not making assumptions and writing algorithms out of thin air, but instead of trying to generate data-sets and observe them.
That, to me, is the real lesson for everybody: we have to look at data more, now that it's increasingly easy to generate and explore it.
That, to me, is the real lesson for everybody: we have to look at data more, now that it's increasingly easy to generate and explore it.
Deep learning then is just one tool, that sometimes is exactly what we need but most of the times is not. Most of the times we do know where to look. We do not have huge problems in many dimensions. And in these cases very simple techniques can work wonders! Chances are that we don't even need neural networks, they are not in general that special.
Maybe we needed just a couple of parameters and a linear regressor. Maybe a polynomial will work, or a piecewise curve, or a small set of Gaussians. Maybe we need k-means or PCA.
Or we can use data just to prove certain relationships exist to then exploit them with entirely hand-crafted algorithms, using machine learning just to validate an assumption that a given problem is solvable from a small number of inputs... Who knows! Explore!
Links for further reading.
- This is a good DNN tutorial for beginners.
- NN playground is fun.
- Keras is a great python DNN framework.
- Alan Wolfe at Blizzard made some very nice blog posts about NNs.
- You should in general know about data visualization, dimensionality reduction, machine learning, optimization & fitting, symbolic regression...
- A good tutorial on deep reinforcement learning, and one on generative adversarial networks.
- History of DL
- DL reading list. Most cited DNN papers. Another good one.
- Differentiable programming, applies gradient descent to general programming.
Links for further reading.
- This is a good DNN tutorial for beginners.
- NN playground is fun.
- Keras is a great python DNN framework.
- Alan Wolfe at Blizzard made some very nice blog posts about NNs.
- You should in general know about data visualization, dimensionality reduction, machine learning, optimization & fitting, symbolic regression...
- A good tutorial on deep reinforcement learning, and one on generative adversarial networks.
- History of DL
- DL reading list. Most cited DNN papers. Another good one.
- Differentiable programming, applies gradient descent to general programming.
Thanks to Dave Neubelt, Fabio Zinno and Bart Wronski
for providing early feedback on this article series!

No comments:
Post a Comment